Do you use floating-point numbers? Should you be using them? If you're not sure, then you probably shouldn't be. Do you know enough about them to use them properly? Again, if you're not sure, you probably don't.

Floating-point numbers should not be used to represent money. It's genuinely frightening how many good software developers are surprised by this statement. One problem that's often pointed out is that you can't represent 0.01 perfectly as a floating-point number. That's true (at least for binary floating-point formats), and by itself it's a good reason not to use floats to represent money[1]. But there's a more general principle at work here: floating-point numbers should not be used to count discrete objects. If you're counting things, be they pennies, candy bars, or EmployeeRecords, you should be using an integer type.

Floating-point types only really work well when you use them to represent measurements of continuous quantities, like length, temperature, or velocity. Think physics, not accounting. As long as you start with continuous quantities and apply only continuous functions to them, floating-point numbers are great. This is what they were designed for.

But you still need to know how to use them. So if you find yourself in a field where floating-point arithmetic is important, you would do well to read up on the subject. Unless you actively reeducate yourself, your intuition for arithmetic is going to lead you astray because your intuition was developed working with real numbers in elementary math classes. Unfortunately for you, floating-point numbers don't quite work the way real numbers do. Certainly not to the extent that machine integers work like actual integers. With machine integers, the only thing that your mathematical intuition is unprepared for is overflow[2]. So long as you avoid overflow, machine integers will work exactly the way you expect.

Not so with floats. If you do anything remotely interesting with them, you just can't escape the fact that they're very different from real numbers, or even rational numbers. If you're working with floating-point numbers, and you're not absolutely sure that you know everything you need to know about them, you need to study them so that you're not surprised by facts like the following.

Fact: There is no floating point number 0.1.

This is mildly confusing for a lot of people because you can type 0.1 as a literal inside a program, or read it from a config file, and it seems to show up correctly. If you try to print the result, it will probably print out as 0.1. But it's not really 0.1. If you print it out with sufficient precision, you'll find that even though your config file said “0.1”, what you actually have in memory is 0.1000000015.

If you really need a floating-point number that's exactly 0.1, then you're out of luck. There is no such beast, and nothing you say or do can make it exist. Well, you could buy or build hardware that implements base-10 floating-point, or you could emulate base-10 floating-point (slowly) in software. If neither of those options appeals to you, then it's time make a decision: if you want to use a floating-point number, then you can't have a number that's exactly 0.1, and if you want to have exactly 0.1, then you can't use a floating-point number. You can't have both.

If you “need” the number to be exactly 0.1 because you're modeling some physical situation in which one thing is exactly 10% of some other thing, then just go ahead and use the floating-point 0.1. It won't be exactly 0.1, but your model won't notice. (Unless it's a chaotic system, in which case any number of small inaccuracies are likely to cause problems, and you may need to rethink your whole approach.)

On the other hand, if you “need” the number to be exactly 0.1 for some legal reason, floating-point numbers are just not the right tool, no matter how much you think they should be. If you're facing possible lawsuits for using 10.00000015% instead of 10%, you need to look into fixed-point arithmetic or maybe arbitrary-precision rationals.

Fact: You can increment (add one to) a floating-point number, and get a result that's exactly the same as the original number.

To illustrate the problem, let's work with base 10, and let's use less precision than you'd actually get from a 32-bit float. This won't change the nature of the problem. It'll just make it easier to see. Every floating point format has some fixed number of digits (usually bits) of available precision. For our example, let's say we have three digits of precision. That means that all of our numbers will look like 0.xyz * 10^e, where x, y, and z are all digits between 0 and 9, and e is some exponent.|normalization| That's how floating-point numbers work in your computer, too, except that they have 24 (or 53 for doubles) bits of precision, and the base of the exponent is 2 instead of 10.

Now let's say you add 0.001 (or .001E0) to 1.0 (.100E1). The answer, of course, is 1.001. But that result has four important digits, and our format can only hold three. So we have to drop the least significant digits until we get to a number we can actually represent, and we end up with 1.00. So we've added two non-zero, positive numbers, and gotten one of the original numbers back as the sum.

It's not hard to do the same with numbers that are all greater than one. Consider 1000 + 1 (or .100E4 + .100E1). Here we end up with 1001, which again has four important digits (exactly the same digits as the previous example, in fact—just with the decimal point in a different spot). To get down to three significant digits so we can fit within our precision, we need to lose the 1 in the least significant place, and we end up with 1000 (or .100E4), which was the number we started with.

Now, a 32-bit float has 24 bits of precision, so the first integer you run into that equals itself when incremented by one is 16,777,216. But that doesn't mean you're safe as long as you stay below that number. The more general problem shown above exists at all levels. If you add together numbers that are farther apart than the amount of precision you have, one of them will just disappear. This has some surprising consequences, such as:

Fact: If you add up a list of floating point numbers both forward and backward, you might get different answers.

What's more, neither forward nor backward is necessarily right. If you're able to, your best bet is to sort the numbers so that you're adding the smallest ones first. This is a result of the property above, that adding together a small floating point number and a large floating point number can end up giving back the larger number as a result, as if the smaller number were zero.

Let's go back to our three-digit decimal floating-point format. We saw above that 1000 + 1 == 1000 in this format. More generally, once you've got a number than greater than 1000, adding any single-digit number to it won't change it, because the ones digit is now outside of the available precision. Now suppose you had tho following list of numbers to add up:

[ 4, 497, 4, 504, 9]

If you add this up from left to right (using only three digits of precision), you'll find that you get 1000. If you add from right to left, though, you'll get 1010. On the other hand, sorting and adding from smallest to largest will give you 1020, which is actually closest to the correct answer of 1018 (and the closest you can get to the correct answer using only three significant digits).

Now, that list might look contrived to you, but that's just because I wanted to make it easy to follow along with your own calculations at home. Consider this one instead:

[4, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 17, 4, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 9 ]

This will give you the same results: 1000 left to right, 1010 right to left, and 1020 sorted (the exact sum is still 1018) . This isn't some bizarre phenomenon that occurs only with unusual, high-variance numeric sequences. You can run into this problem even with fairly ordinary looking lists of floating-point numbers.

Fact: There is a floating-point number that's bigger than std::numeric_limits<float>::max().

In C++, std::numeric_limits<float>::max() represents the largest finite float. What some people don't realize is that there are also floating-point bit patterns which represent infinite values. So checking whether a float is bigger than ::std::numeric_limits<float>::max() is basically telling you whether it's infinite. It's possible to have code that does this to check for overflow at some key step, so that it can use a floating-point type with greater precision in those cases.

Fact: There is a floating-point value that's not equal to itself.

It's called NaN (Not-a-Number), and it's what you get if you try to divide zero by zero, or divide infinity by infinity, or subtract infinity from infinity. Since it's not a number, it's not valid to use it in numeric comparisons, and it's not considered equal to anything—not even itself.

I once forgot about this, and it cost me hours (spread over several weeks) spent in debugging a unit test for a copy constructor. The test was filling a matrix with random bits, then making a copy of the matrix and checking that it was equal to the first matrix. On certain machines, with certain compiler flags, this test failed. I read through websites, language standards, and assembly listing trying to figure out what could be going wrong. When I eventually managed to sit down in front of a machine where the bug occurred and printed out the matrix, only to be faced with a NaN, it was a serious facepalm moment.

On the flip side, there are two distinct floating-point numbers with different bit patterns that are nonetheless equal to each other. The IEEE floating-point format uses the first bit to indicate sign, so +0.0 and -0.0 have different bit patterns, and even behave differently in arithmetic: if you divide 1.0 by -0.0, you get negative infinity, but if you divide 1.0 by +0.0, you get positive infinity. But both numbers are still zero, so they're considered equal in numeric comparisons.

Fact: On some machines (including x86), your intermediate calculations are probably being done at a different precision than your final results.

The x86 FPU (Floating-Point Unit) works with 80-bit extended precision floating-point numbers by default. If you have an expression that involves only 64-bit doubles, chances are that most of the math will be done using 80-bit long doubles. This is largely harmless, but it can cause real problems when debugging because it can introduce inconsistencies between optimized and unoptimized code.

Unoptimized code tends to interact with memory a lot, storing values from registers into memory, and then loading them back from memory into a register almost immediately. Optimized code tries to avoid talking to memory (because it's really slow), attempting instead to keep values in registers as much as possible. In the case of floating-point numbers on x86, this means they're staying in 80-bit registers, rather than being stored back into a 64-bit memory location.

So with optimization turned on, you get not only better performance, but also more precision. Sounds great, right? Well, yeah, I guess it is pretty cool. But it can occasionally make debugging a real pain in the neck, because you get different answers from optimized and unoptimized code.

Fact: Many floating-point arithmetic settings are controlled by global variables (often some control register) that library calls can screw with.

I used to work on medical software where we explicitly set the system to throw an exception on floating-point errors (underflow, overflow, divide-by-zero) because we wanted to find out right away when something failed. Then one day it stopped working.

It took us a while to notice, and it took even longer to track it down. It turns out that the version of Microsoft's XML parser we were using was turning off floating-point exceptions while it parsed the file (which is fine), and failing to restore our original settings when it was done (which is Bad).

And exceptions aren't the only floating-point behavior that's both global and mutable. Depending on your hardware, so are rounding modes, or even precision.

Fact: Many numbers, including a wide range of integers, can be represented exactly using floating-point numbers

Once people become aware of the issues I've pointed out above, they often get skittish about floating-point numbers in general. It's certainly good to exercise caution, but too many programmers seem to regard floating-point numbers as some sort of nebulous things that never have any exact value. That's just wrong.

Every floating-point number represents some precise numeric value (except for NaN, which is explicitly not a number). Powers of two can often be represented exactly, as can many integer multiples of powers of two. In particular, since 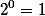2^0=1, integers themselves can be precisely represented, up to the size of the significand in your floating-point format.

This means, for example, that 64-bit doubles can exactly represent more (many more) integers than a 32-bit integer type. Since doubles have a 53-bit significand, a 53-bit integer can be represented exactly using a double.

More generally, if you actually learn how floating-point numbers work, you'll find that the IEEE standard makes lots of useful guarantees, and you can reason about them successfully. You just have to keep in mind that they're not real numbers—they're a finite-precision approximation of real numbers.

Fact: You can get from one floating-point number to the next highest one by treating it like an integer and incrementing it.

This isn't so much a gotcha as a fun fact, and one that's occasionally useful to know. It provides an easy way to gauge the distance between floating-point numbers at a given spot on the number line. (The distance between consecutive floats varies, because they're not evenly distributed. For example, there are as many floats between 1 and 2 as there are between 2 and 4, so floats between 1 and 2 are twice as close together.) Just treat the number as an integer, increment that bit pattern, and see how close it is to the previous floating-point number.

The syntax to do this in C gets pretty hairy. If you just cast from a float to an int, you'll get a numeric conversion instead of keeping the same bit pattern.[3] Assuming that floats and ints are the same size (in bytes), you need to do this: float next = *((float*)&(*((int*)&f)) + 1);.[4]

So now do you know everything you need to know about floating-point numbers? By no means. That wasn't the point of this post. The point of this post was to convince you that you need to learn more about them (or else not use them at all). The place to start is What Every Computer Scientist Should Know About Floating-Point Arithmetic. It's long, and it's pretty math-heavy, but it'll tell you what you need to know.