Every so often, I hear about interviewers asking job-seekers to write a function to compute factorials, and I'm forced to wonder why anyone would ask that. I mean, I realize that the interviewer is trying to figure out whether the candidate has ever heard of recursion (or maybe whether the candidate can write code at all). But asking someone to write a factorial function is just inviting them to spew buggy and inefficient code onto a whiteboard. And in most cases, the interviewers apparently don't notice that there's anything wrong with it.
First, let's review what the factorial is. The factorial is a function from the nonnegative integers to the positive integers defined by the recurrence:
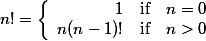
It's pretty obvious how to write a recursive function to implement this. If you've ever written a recursive function before in your life, you can figure out how to craft a recursive function to compute n!, which probably explains the popularity of the question. But just to make sure we haven't left anybody out, let's write up a solution in C++. If an interviewer asks you to write a C++ function to compute n!, they almost certainly want to see something like this on their whiteboard:
// Recursive factorial implementation (buggy and inefficient)
int factorial(int const n)
{
if (n < 0)
{
std::ostringstream err;
err << "Cannot compute factorial of negative value " << n;
throw std::runtime_error(err.str());
}
if (n == 0)
{
return 1;
} else {
return n * factorial(n-1);
}
}
Now, one problem with asking this question to see if somebody knows about recursion is that the naïve recursive solution is needlessly inefficient. The implementation above is linear in both time and space, but it's easy to transform it into an iterative algorithm that's still linear in time but uses constant space:
// Iterative factorial implementation (more efficient, but still buggy)
int factorial(int const n)
{
if (n < 0)
{
std::ostringstream err;
err << "Cannot compute factorial of negative value " << n;
throw std::runtime_error(err.str());
}
int ret = 1;
for (int i = 2; i <= n; ++i)
{
ret *= i;
}
return ret;
}
Of course, this implementation (and the one before it) is buggy. It's a serious problem just waiting to happen. Take a minute to look at it and see if you can spot the bug.
The problem is that factorials are big. Really big. You just won't believe how amazingly big factorials are. The factorial grows faster than 2n. In fact, it grows faster than bn for any constant base b. The upshot of this is that since the int on many C++ compilers is 32 bits wide, the largest input for which you can actually return the correct result is (wait for it...) 12. That's right: 13! is larger than 232, so it won't fit in 32 bits. So why bother computing a result at all? Just store the 13 valid answers in an array, and index into it. If you ever really need to write a factorial function that returns a 32-bit int, I recommend the following code:
// Efficient, bug-free factorial implementation
int factorial(int const n)
{
if (n < 0)
{
std::ostringstream err;
err << "Cannot compute factorial of negative value " << n;
throw std::runtime_error(err.str());
}
static int facts[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600};
if (n >= (sizeof(facts)/sizeof(facts[0])))
{
std::ostringstream err;
err << "Factorial of " << n << " is too large to fit in a " << sizeof(facts[0]) << "-byte integer";
throw std::runtime_error(err.str());
}
return facts[n];
}
This code is superior to the original recursive solution in three ways:
- It uses constant memory
- It runs in constant time
- It throws an exception for inputs that are too large, whereas the original results in undefined behavior
But wait, you say, what if we return a 64-bit integer type instead? With 64 bits instead of 32, we could indeed represent more factorials. Keep in mind, though, that n! grows much faster than 2n, so doubling the number of bits in our integer doesn't actually buy us much. Using a 64-bit integer you could return correct values for inputs up to 20. Still not much reason to compute an answer instead of just indexing into a pre-populated array. Using 128 bits will get you as far as 34!, which isn't that much higher, but might be getting high enough that you'd be nervous about just putting an array of results into your code. Hold onto that thought—I'll come back to it.
In Java, at least, there's BigInteger. Maybe when interviewers ask candidates to write a factorial function in Java, the question is intended to gauge their knowledge of little-used portions of the standard library, and these interviewers are secretly hoping to see some BigInteger computations on the whiteboard. But I doubt it.
You can actually get some decent mileage out of floating-point numbers. By design, they sacrifice accuracy in less significant digits in order to get roughly the right answer across a wide range of numbers. While 32-bit floats aren't big enough to be much of an improvement over ints, a 64-bit float can give you answers that are at least the right order of magnitude for inputs well over a hundred, and after 170, you'll get infinity, which is honestly a pretty good approximation for 171!.
This brings up an important question: What are these factorials going to be used for? Do we need to return an int? Would it be okay to return an arbitrary-precision integer (like Java's BigInteger), risking substantial heap allocation for large inputs? Is it okay for us to return a floating-point number that's close to the right answer but not always exactly right? What's the purpose of computing these factorials anyway?
In the vacuum of an interview, of course, none of these questions have real answers beyond whatever arbitrary constraints the interviewer makes up. But in the real world, what would we need to compute a factorial for?
One thing you would certainly use factorials for is combinatorics. If you want to calculate the number of different seven-card hands you could draw from a deck of cards, for example, you're going to run straight into some factorials. They'll be big numbers, too (like 45!), so using a fixed-size integer type is no good. You also don't want to use floating-point numbers. When you're calculating permutations and combinations, you're going to need lots of factors to cancel during division, and it's not going to work out right if you use floating-point arithmetic[1]. So you probably use some arbitrary-precision integers and accept a little verbosity and inefficiency. To be honest, if you're doing lots of factorials for combinatorics, you might well be better off returning some sort of optimized multiset of the number's factors instead of a more standard-looking numeric type.
Another major use-case for factorials would be power series (and similar approximation methods). Here you almost certainly want to return a double, and you probably want to return it quickly. In fact, if you're really worried about efficiency (as people often are when doing numerical stuff involving power series), you probably want to return the reciprocal of n! so that you can turn a (slow) division into a (relatively fast) multiplication for each term in your series. So the ideal implementation would probably index into a precomputed array of 171 doubles representing the reciprocals of the 171 factorials that can fit in a double[2] and just return zero for any input over 170.
The downside of such an implementation (and any implementation that just indexes into a pre-computed array) would be that it does not actually encode an algorithm for computing the factorials. That's fine as far as running the code goes, since you don't actually want to waste time running the algorithm. But it's a disaster for reusability, maintainability, and debugging. An implementation that indexes into an array of 171 doubles is deeply tied to the double type—you'll need a different function for 32-bit floats or 80-bit extended precision doubles. Worse, the next person who looks at the code just has to assume that all 171 values in that array are accurate (at least, as accurate as possible within the framework of floating-point numbers). Worst of all, if one of the values contains a typo, it's entirely possible that nobody will notice until a satellite goes off course or a missile lands in the wrong place. And, boy, will your face be red then.
So what's the solution? I think the ideal would be to have code that implements the factorial algorithm, but to run that code at compile time to create the array that will be used for looking up results at runtime. Using some templates and Boost's preprocessor library, this is actually not that hard to do in C++. Like many things in C++, however, it is fairly ugly:
#include <boost/preprocessor/arithmetic/inc.hpp>
#include <boost/preprocessor/comparison/not_equal.hpp>
#include <boost/preprocessor/repetition/for.hpp>
#include <boost/preprocessor/tuple/elem.hpp>
#include <boost/preprocessor/punctuation/comma_if.hpp>
template <int N>
struct FactInv
{
const static double value = (1.0/N) * FactInv<N-1>::value;
};
template < >
struct FactInv<0>
{
const static double value = 1.0;
};
#define PRED(r, state) \
BOOST_PP_NOT_EQUAL( \
BOOST_PP_TUPLE_ELEM(2, 0, state), \
BOOST_PP_INC(BOOST_PP_TUPLE_ELEM(2, 1, state)))
#define OP(r, state) \
(BOOST_PP_INC(BOOST_PP_TUPLE_ELEM(2, 0, state)), \
BOOST_PP_TUPLE_ELEM(2, 1, state))
#define MACRO(r, state) \
FactInv< BOOST_PP_TUPLE_ELEM(2, 0, state) >::value \
BOOST_PP_COMMA_IF(PRED(r,state))
double
fact_inv(int i)
{
static double lut[] = {
BOOST_PP_FOR((0, 170), PRED, OP, MACRO)
};
if (i < (sizeof(lut)/sizeof(lut[0])))
{
return lut[i];
}
return 0.0;
}
The code above would make a lot of people (justifiably) nervous. And the accuracy probably suffers for larger factorials, because it's multiplying the inverses together, when what you'd really want is to compute the factorial exactly using arbitrary-precision integers, and then find the double that's closest to that factorial's reciprocal. The only real upside here is that it's all written in C++. In something like Java, with no compile-time metaprogramming at all, I don't think you can do better than writing a Python script that runs at compile time, computes the lookup table for the factorials, and inserts the table into your program. Whether doing that is cleaner than the C++ code above is probably debatable, but either way, you're stuck with a solution that's not entirely satisfactory. And you won't do any better in most mainstream programming languages, so most people will end up either taking the runtime hit or settling for ugly code.
On the other hand, it's trivial using Lisp macros. The code below even decides for itself when it's hit its limit, rather than relying on a hard-coded 170. Pulling that off at compile time in C++ would be challenging, to say the least.
(defun slow-fact (n)
(if (= n 0)
1
(* n (slow-fact (1- n)))))
(defun slow-fact-inv (n)
(/ 1 (slow-fact n)))
(defmacro make-fact-lut ()
;; Don't let the unfortunate "for ... then" syntax confuse you.
;; translate "then" as "updated on each iteration with"
(let ((lut (loop for n = 0 then (1+ n)
and one-over-n! = 1 then (slow-fact-inv n)
if (> one-over-n! least-positive-normalized-double-float)
collect (coerce one-over-n! 'double-float) into ret
else return ret)))
(make-array (length lut)
:element-type 'double-float
:initial-contents lut)))
(defun fact-inv (n)
(let ((lut (make-fact-lut)))
(if (>= n (length lut))
0
(aref lut n))))
So the next time an interviewer asks you to write a factorial function, go ahead and point out that the correct implementation is highly context dependent, that the answer they're probably hoping to see is buggy, and that creating an efficient solution with clean code is only possible in something like Lisp. On second thought, you probably shouldn't bring up Lisp if you actually want the job.