There are lots of simple tricks to help you check your math. There's a good chance that you already know about casting out nines to check arithmetic and using dimensional analysis to do a sanity check on your models. But there's one technique that I've found useful, but that I've never seen anybody else advocate (possibly because it can make your math look a little goofy). When doing math by hand, I've found that you can avoid lots of silly mistakes by using different alphabets for different types of values. (Warning: You may need a decent Unicode font installed to make sense of the rest of this post.)
This isn't really an unusual idea. We already, for example, using certain Greek letters for angles. We also use capitalization or font differences to denote different things: f is a function, F is (maybe) the Fourier transform of f, 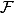 is a filter or ultrafilter,
is a filter or ultrafilter, 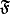 is the Fourier transform operator, and
is the Fourier transform operator, and 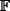 is a field. And it's common practice to put diacritic marks above or below a letter to indicate some characteristic.[1]
is a field. And it's common practice to put diacritic marks above or below a letter to indicate some characteristic.[1]
But although there are a number of conventions for using different characters for different types of values, I don't think we do this sort of thing enough, especially with variables that have similar “types” but appear in different portions of an expression. Let me show you what I mean. There are two errors in the equation below. See if you can spot them.
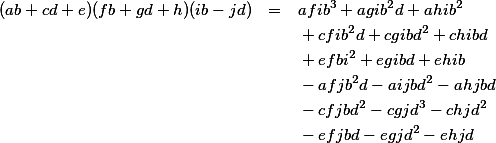
If we adhere to the more usual convention of using letters from the end of the alphabet for our variables, one of the errors becomes more obvious.
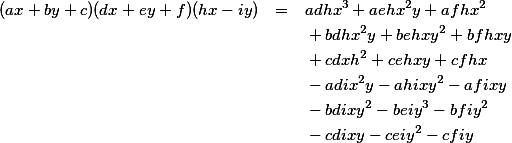
Can you see it? In the first term on the third line, there's an h2, when obviously the only letters that should be squared are x and y.
Now, if we go one step further, and use a different alphabet for each set of coefficients, the other error will pop out.
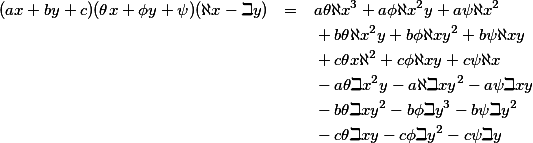
In this last equation, not only do we have the obviously wrong א squared[2] corresponding to the h2 in the second equation, but now we have both א and ב appearing in the same term (on the fourth line). Clearly they should never be in the same term: this is the second error. If you look back at the first equation, you'll see that it also contains both of these errors. They're just a lot harder to spot.
Now, to avoid confusion and make sure errors really stand out, you have to be careful which letters you use. Ideally, you want to choose letters that are unambiguously members of their particular alphabet. This rules out things like the Greek iota, because it look way too much like the Latin character i.
It's also good to have characters that are a single, connected mark, with no spaces. In real life, for example, I would never use the Hebrew Aleph (א) as I did above, because its handwritten form could easily be mistaken for the expression 1c, while a handwritten approximation of the letter's printed block form can too easily end up looking like an x.
For your benefit, I've taken the liberty of listing out some chunks of distinctive characters that can be used for different types of variables.
- a, b, c, d — beginning of Latin alphabet
- i, j, k — “index” portion of Latin alphabet
- x, y, z — end of Latin alphabet
- α, β, γ, δ — beginning of Greek alphabet
- θ, φ, ψ — “angle” portion of Greek alphabet
- я, ж — Cyrillic letters that don't look like either Latin or Greek
- ま, め — distinctive, connected Hiragana syllables starting with m
- さ, す, せ, そ — distinctive, connected Hiragana syllables starting with s
- ゆ, よ — distinctive, connected Hiragana syllables starting with y
- 女, 日, 木, 舌 — a few distinctive Chinese characters that are relatively simple for English speakers to remember
Now if you're unfamiliar with the Asian characters, you probably won't be able to use the different segments for different types of values. You'll be stuck using the whole thing as a single block, or not using it at all. That's okay. I can't use Arabic characters at all—they just look like squiggly lines to me. For that matter, so do Greek ξ and ζ, so I don't use them either if I can avoid it. (Unfortunately, they're sometimes unavoidable. If something looks like I just scribbled randomly on the paper, I usually assume it's a ξ.) But if you are sufficiently familiar with Arabic, or Devanagari, or Tamil, or whatever (you can even make up your own symbols—you don't need that many to be worthwhile), then use it! It'll help you notice stupid mistakes.